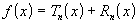x0 = 2
n = 3
Общий вид формулы Тейлора:
для k = 0:
D[x/(x-1), {x, 0}] = x/(x-1)
f(2) = 2/(2-1) = 2
0! = 1
для k = 1:
D[x/(x-1), {x, 1}] = -1/(x-1)^2
f(2) = -1/(2-1)^2 = -1/1 = -1
1! = 1
для k = 2:
D[x/(x-1), {x, 2}] = 2/(x-1)^3
f(2) = 2/(2-1)^3 = 2
2! = 2
для k = 3:
D[x/(x-1), {x, 3}] = -6/(x-1)^4
f(2) = -6/(2-1)^4 = -6/1= -6
3! = 6
(2/1)*(x-2)^0 + (-1/1)*(x-2)^1 + (2/2)*(x-2)^2 + (-6/6)*(x-2)^3 = -(x-2)^3 + (x-2)^2 - x + 4
Форма Лагранжа:
D[x/(x-1), {x, (3+1)}] = 24/(x-1)^5
f(c) = 24/(c-1)^5
(3 + 1)! = 24
( (24/(c-1)^5) / 24) * (x - 2)^(3+1) = ((x-2)^4 / (c-1)^5)
19. Формула Тейлора с остаточным членом в форме Лагранжа и в форме Пеано
