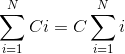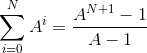При анализе алгоритмов нам придется складывать величины из некоторых наборов величин. Пусть, скажем, у нас есть алгоритм с циклом. Если переменная цикла принимает значение 5, то цикл выполняется 5 раз, а если её значение равно 20, то двадцать. Вообще, если значение переменной цикла равно M, то цикл выполняется M раз. В целом если переменная цикла пробегает все значения от 1 до N, то суммарное число выполнений цикла равно сумме всех натуральных чисел от 1 до N. Мы записываем эту сумму в виде 
. В нижней части знака суммы стоит начальное значение переменной суммирования, а в его верхней части - её конечное значение. Понятно, как такое обозначение связано с интересующими нас суммами.
Если какое-нибудь значение записано в виде подобной суммы, то его зачастую стоит упростить, чтобы результат можно было сравнивать с другими подобными выражениями. Не так уж просто сообразить, какое из двух чисел больше
и 
.
Поэтому для упрощения сумм мы будем пользоваться нижеследующими формулами, в которых C - не зависящая от i постоянная.
; (1.8)
; (1.9)
; (1.10)
; (1.11)
. (1.12)
Равенство означает просто, что сумма чисел от 0 до N равна сумме чисел от N до 0. В некоторых случаях применение этого равенства упрощает вычисления.
; (1.13)
; (1.14)
. (1.15)
Равенство легко запомнить, если разбить числа от 1 до N на пары. Складывая 1 с N, 2 с N-1 и т.д., мы получим набор сумм, каждая из которых равна N+1. Сколько всего будет таких сумм? Разумеется, их число равно половине числа разбиваемых на пары элементов, т.е. N/2. Поэтому сумма всех N чисел равна
.
; (1.16)
. (1.17)
Равенство легко запомнить через двоичные числа. Сумма степеней двойки от нулевой до десятой равна двоичному числу 11111111111. Прибавив к этому числу 1, мы получим 100000000000, т.е. 211. Но этот результат на 1 больше суммы степеней двойки от нулевой до десятой, поэтому сама сумма равна 211 - 1. Если теперь вместо 10 подставить N, то мы придем к равенству .
для любого числа A; (1.18)
; (1.19)
; (1.20)
. (1.21)
При упрощении сумм можно сначала разбивать их на более простые суммы с помощью равенств (1.8)-(1.12), а затем заменять суммы с помощью остальных тождеств.
. В нижней части знака суммы стоит начальное значение переменной суммирования, а в его верхней части - её конечное значение. Понятно, как такое обозначение связано с интересующими нас суммами.Если какое-нибудь значение записано в виде подобной суммы, то его зачастую стоит упростить, чтобы результат можно было сравнивать с другими подобными выражениями. Не так уж просто сообразить, какое из двух чисел больше
и .Поэтому для упрощения сумм мы будем пользоваться нижеследующими формулами, в которых C - не зависящая от i постоянная.
; (1.8); (1.9); (1.10); (1.11). (1.12)Равенство
означает просто, что сумма чисел от 0 до N равна сумме чисел от N до 0. В некоторых случаях применение этого равенства упрощает вычисления.; (1.13); (1.14). (1.15)Равенство легко запомнить, если разбить числа от 1 до N на пары. Складывая 1 с N, 2 с N-1 и т.д., мы получим набор сумм, каждая из которых равна N+1. Сколько всего будет таких сумм? Разумеется, их число равно половине числа разбиваемых на пары элементов, т.е. N/2. Поэтому сумма всех N чисел равна
.; (1.16). (1.17)Равенство
легко запомнить через двоичные числа. Сумма степеней двойки от нулевой до десятой равна двоичному числу 11111111111. Прибавив к этому числу 1, мы получим 100000000000, т.е. 211. Но этот результат на 1 больше суммы степеней двойки от нулевой до десятой, поэтому сама сумма равна 211 - 1. Если теперь вместо 10 подставить N, то мы придем к равенству . для любого числа A; (1.18); (1.19); (1.20). (1.21)При упрощении сумм можно сначала разбивать их на более простые суммы с помощью равенств (1.8)-(1.12), а затем заменять суммы с помощью остальных тождеств.
