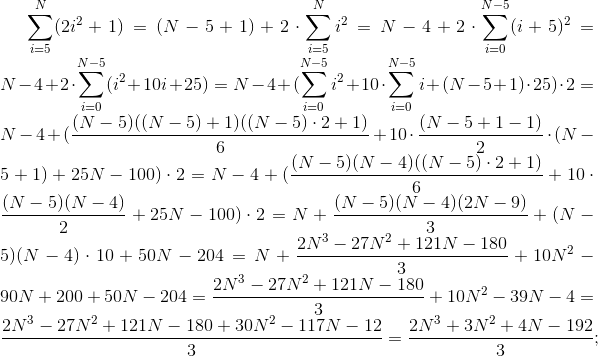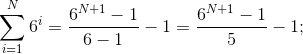Упражнения по анализу алгоритмов

1.1.3.1

Напишите на псевдокоде алгоритм, подсчитывающий количество прописных букв в текстовом файле. Сколько сравнений требуется этому алгоритму? Каково максимальное значение числа операций увелечения счетчика? Минимальное такое число? (Выразите ответ через число N символов во входном файле.)

Тут и далее в решениях вместо псевдокода будет использоваться код на каком-нибудь формальном языке программирования. При желании его легко можно преобразовать в псевдокод опустив несущественные подробности.

Алгоритм на языке программирования Си подсчитывающий количество прописных букв в текстовом файле:

#include <stdio.h>

int main(void)
{
    FILE *fp;
    int c, cnt = 0;

    fp = fopen("datafile.txt", "r");

    while ((c = fgetc(fp)) != EOF)
    {
        if (c >= 'A' && c <= 'Z')
        {
            cnt++;
        }
    }

    printf("%d\n", cnt);

    fclose(fp);

    return 0;
}

В языке программирования Си значения булевых выражений вычисляются сокращенным образом. В выражении c >= 'A' && c <= 'Z', член c <= 'Z' вычисляется только, если выражение c >= 'A' истинно.
Если считать, что булевы выражения вычисляются сокращенным образом, то число сравнений требуемых этому алгоритму находится между N и 2N. Если в текстовом файле не будет ни одной прописной буквы, то алгоритму потребуется N сравнений. Если все символы в текстовом являются прописными буквами, то алгоритму потребуется 2N сравнений.
Вообще для анализа алгоритмов это неважно считать ли число сравнений при проверке сложного условия равным 1 или 2.

Максимальное значение числа операций увеличения счетчика равно N. Если все символы в текстовом являются прописными буквами, то всего будет сделано N операцией увеличения счетчика.

Минимальное значение числа операций увеличения счетчика равно 0. Если в текстовом файле не содержится прописных букв, то не будет сделано ни одной операции увеличения счетчика.

См. также:

1.1.3.2

В файле записано несколько чисел, однако мы не знаем, сколько. Напишите на псевдокоде алгоритмы для подсчета среднего значения чисел в файле. Какого типа операции делает ваш алгоритм? Сколько операций каждого типа он делает?

Алгоритм на языке программирования Ruby подсчитывающий среднее значение чисел в файле:

#!/usr/bin/ruby -w

counter = 0
sum = 0.0
file = File.new("datafile.txt", "r")
while (line = file.gets)
    sum += line.to_i
    counter += 1
end
file.close
avg = sum / counter
puts "#{avg} = #{sum} / #{counter}"

Всего операций:
  • 2N + 5 присваиваний:
    • 3 присваивания при инициализации переменных counter, sum, и file;
    • N + 1 присваиваний переменной line;
    • N присваиваний результата сложения переменной sum и прочитанного числа;
    • 1 присваивание результата деления переменной sum на counter;
  • 2N + 1 арифметических операций:
    • 2N аддитивных операций:
      • N операций сложения переменной sum и прочитанного числа;
      • N приращений переменной counter в цикле чтения из файла;
    • 1 мультипликативная операция:
      • 1 операция деления переменной sum на counter;
  • N + 1 операций сравнения:
    • N + 1 проверок условия в цикле чтения из файла (+1 для последней проверки, когда файл пуст).

1.1.3.3

Напишите алгоритм, не использующий сложных условий, который по трем введенным целым числам определяет, различны ли они все между собой. Сколько сравнений в среднем делает ваш алгоритм? Не забудьте исследовать все классы входных данных.

Алгоритм на языке сценариев (скриптов) командной оболочки bash, определяющий по трем введенным целым числам, различны ли они все между собой:

#!/bin/bash

first_num=0
second_num=0
third_num=0

echo -n "Enter the first number --> "
read first_num
echo -n "Enter the second number -> "
read second_num
echo -n "Enter the third number --> "
read third_num

if [[ "$first_num" -ne "$second_num" ]]; then
    if [[ "$first_num" -ne "$third_num" ]]; then
        if [[ "$second_num" -ne "$third_num" ]]; then
            echo "YES"
        else
            echo "NO"
        fi
    else
        echo "NO"
    fi
else
    echo "NO"
fi

Классы входных данных
В среднем алгоритм делает 2 сравнения.

1.1.3.4

Напишите алгоритм, который получает на входе три целых числа, и находит наибольшее из них. Каковы возможные классы входных данных? На каком из них ваш алгоритм делает наибольшее число сравнений? На каком меньше всего? (Если разницы между наилучшими и наихудшими классами нет, перепишите свой алгоритм с простыми сравнениями так, чтобы он не использовал временных переменных и чтобы в наилучшем случае он работал быстрее, чем в наихудшем.)

Алгоритм на языке программирования Pyhton, находящий наибольшее из трёх введённых чисел:

#!/usr/local/bin/python

a = int(input("Enter the first  number: "))
b = int(input("Enter the second number: "))
c = int(input("Enter the third  number: "))

if a > b:
    if a > c:
        print a
    else:
        print c
else:
    if b > c:
        print b
    else:
        print c

To be continued...

1.1.3.5

Напишите алгоритм для поиска второго по величине элемента в списке из N значений. Сколько сравнений делает ваш алгоритм в наихудшем случае? (Обсуждение алгоритма, которому требуется около N сравнений.)

1.2.2.1

Напишите алгоритм подсчета среднего значения, или медианы, трех целых чисел. Входные данные для такого алгоритма распадаются на шесть групп; опишите их. Какой случай для алгоритма является наилучшим? Наихудшим? Средним? (Если наилучший и наихудший случаи совпадают, то перепишите Ваш алгоритм с простыми условиями, не пользуясь временными переменными, так, чтобы наилучший случай был лучше наихудшего.)

1.2.2.2

Напишите алгоритм, проверяющий, верно ли, что данные четыре целых числа попарно различны. Деление на группы возможных наборов входных данных зависит от структуры Вашего алгоритма либо от структуры задачи. Какой из классов обеспечивает наилучший случай для Вашего алгоритма? Наихудший? Средний? (Если наилучший и наихудший случаи совпадают, то перепишите Ваш алгоритм с простыми условиями, не пользуясь временными переменными, так, чтобы наилучший случай был лучше наихудшего.)

1.2.2.3

Напишите алгоритм, который по данному списку чисел и среднему значению этих чисел определяет, превышает ли число элементов списка, больших среднего значения, число элементов, меньших этого значения, или наоборот. Опишите группы, на которые распадаются возможные наборы входных данных. Какой случай для алгоритма является наилучшим? Наихудшим? Средним? (Если наилучший и наихудший случаи совпадают, то перепишите Ваш алгоритм так, чтобы он останавливался, как только ответ на поставленный вопрос становится известным, делая наилучший случай лучше наихудшего.)
Строго говоря, решение этой задачи зависит от того, знаем ли мы заранее длину входных данных или она выясняется в процессе работы алгоритма.

1.3.5.1

Типичный калькулятор умеет вычислять натуральные логарифмы (по основанию е) и логарифмы по основанию 10. Как с помощью этих операций вычислить log2759?

log2759 = ln59 / ln27 = 4,07753744390572   / 3,295836866004329 = 1,23717817649424
log2759 = lg59 / lg27 = 1,770852011642144 / 1,431363764158987 = 1,23717817649424

1.3.5.2

Допустим, у нас есть честная кость с пятью гранями, на которых написаны числа от 1 до 5. Какова вероятность выпадения каждого из чисел 1, ..., 5 при бросании кости? В каком диапазоне могут меняться суммы значений при бросании двух таких костей? Какова вероятность появления каждого из чисел в этом диапазоне?

1.3.5.3

Допустим, у нас есть честная 8-гранная кость, на гранях которой написаны числа 1,2,3,3,4,5,5,5. Какова вероятность выбросить каждое из чисел от 1 до 5? В каком диапазоне могут меняться суммы значений при бросании двух таких костей? Какова вероятность появления каждого из чисел в этом диапазоне?

1.3.5.4

На гранях четырех кубиков написаны такие числа:
  • d1: 1,2,3,9,10,11;
  • d2: 0,1,7,8,8,9;
  • d3: 5,5,6,6,7,7;
  • d4: 3,4,4,5,11,12.
Вычислите для каждой пары кубиков вероятность того, что на первом кубике выпадет большее значение, чем на втором, и наоборот. Результаты удобно представлять в виде (4 х 4)-матрицы, в которой строчка соответствует первому кубику, а столбец — второму. (Мы предполагаем, что бросаются разные кубики, поэтому диагональ матрицы следует оставить пустой.) У этих кубиков есть интересные свойства — обнаружите ли вы их?

1.3.5.5

На столе лежат пять монет. Вы переворачиваете случайную монету. Определите для каждого из четырех приведенных ниже случаев вероятность того, что после переворота решка будет на
большем числе монет.
  • а. Два орла и три решки 
  • б. Три орла и две решки 
  • в. Четыре орла и одна решка
  • г. Один орел и четыре решки

1.3.5.6

На столе лежат пять монет. Вы переворачиваете один раз каждую монету. Определите для каждого из четырех приведенных ниже случаев вероятность того, что после переворота решка будет на большем числе монет.
  • а. Два орла и три решки 
  • б. Три орла и две решки 
  • в. Четыре орла и одна решка
  • г. Один орел и четыре решки

1.3.5.7

Найдите эквивалентное представление следующих выражений, не содержащее знака суммы:

а) ;

 б) ;

 в) ;

 г) ;

 д) ;

 е) .

а) Сумма первых n членов арифметической прогрессии , где a1 — первый член прогрессии, d — разность прогрессии, n — количество суммируемых членов.

\sum_{i=1}^{n}(3i+7)=\frac{(3+7)\cdot2+(n-1)\cdot3}{2}\cdot n=\frac{20+3n-3}{2}\cdot n=\frac{3n+17}{2}\cdot n;

б)

\sum_{i=1}^{N}(i^{2}-2i)=\sum_{i=1}^{N}i^{2}-\sum_{i=1}^{N}2i=\frac{N(N+1)(2N+1)}{6}-\frac{4+2(N-1)}{2}\cdot N=\frac{2N^{3}+3N^{2}+N}{6}-\frac{2N^{2}+2N}{2}=\frac{2N^{3}-3N^{2}-5N}{6};

в)

\sum_{i=7}^{N}i=\sum_{i=0}^{N-7}(i+7)=\frac{2\cdot 7+(N-7-1+1)\cdot 1}{2}\cdot (N-7+1)=\frac{14+(N-7)}{2}\cdot (N-6);

г) Одно из свойств определённой суммы .

\sum_{i=5}^{N}(2i^{2}+1)=(N-5+1)+2\cdot \sum_{i=5}^{N}i^{2}=N-4+2\cdot \sum_{i=0}^{N-5}(i+5)^{2}=N-4+2\cdot \sum_{i=0}^{N-5}(i^{2}+10i+25)=N-4+(\sum_{i=0}^{N-5}i^{2}+10\cdot \sum_{i=0}^{N-5}i+(N-5+1)\cdot 25)\cdot 2=N-4+(\frac{(N-5)((N-5)+1)((N-5)\cdot 2+1)}{6}+10\cdot \frac{(N-5+1-1)}{2}\cdot (N-5+1)+25N-100)\cdot 2=N-4+(\frac{(N-5)(N-4)((N-5)\cdot 2+1)}{6}+10\cdot \frac{(N-5)(N-4)}{2}+25N-100)\cdot 2=N+\frac{(N-5)(N-4)(2N-9)}{3}+(N-5)(N-4)\cdot10+50N-204=N+\frac{2N^{3}-27N^{2}+121N-180}{3}+10N^{2}-90N+200+50N-204=\frac{2N^{3}-27N^{2}+121N-180}{3}+10N^{2}-39N-4=\frac{2N^{3}-27N^{2}+121N-180+30N^{2}-117N-12}{3}=\frac{2N^{3}+3N^{2}+4N-192}{3};

д)

\sum_{i=1}^{N}6^{i}=\frac{6^{N+1}-1}{6-1}-1=\frac{6^{N+1}-1}{5}-1;

е)

\sum_{i=7}^{N}4^{i}=\frac{4^{N+1}-1}{4-1}-\frac{4^{6+1}-1}{4-1}=\frac{4^{N+1}-1}{3}-5461.

1.4.2.1

Расположите следующие функции в порядке возрастания скорости роста. Если некоторые из них растут с одинаковой скоростью, то объедините их овалом.
2n;         log2log2n;      n3 + log2n;       log2n;          n - n2 + 5n3;
2n-1;      n2;                  n3;                   nlog2n;        (log2n)2;
√n;        6;                    n!;                    n;                (3/2)n.

1.4.2.2

Для каждой из приведенных ниже пар функций f и g выполняется одно из равенств: либо f = О(g), либо g = О(f), но не оба сразу. Определите, какой из случаев имеет место.
а) f(n) = (n2 - n)/2,       g(n) = 6n;
б) f(n) = n + 2√n,         g(n) = n2;
в) f(n) = n + nlog2n,     g(n) = n√n;
г) f(n) = n2 + 3n + 4,    g(n) = n3;
д) f(n) = nlog2n,           g(n) = n√n/2;
е) f(n) = n + log2n,       g(n) = √n;
ж) f(n) = 2log2n2,         g(n) = log2n + 1;
з) f(n) = 4nlog2n + n,   g(n) = (n2 - n)/2.

1.5.2.1

Нарисуйте дерево турнира для следующего набора значений: [14, 3, 10, 7, 13, 4, 15, 5, 6, 22, 16, 1, 8, 2, 9, 12]. Какие элементы будут сравниваться на втором этапе поиска второго по величине значения?

1.5.2.2

Нарисуйте дерево турнира для следующего набора значений: [13, 1, 12, 3, 9, 5, 2, 11, 10, 8, 6, 4, 7]. Какие элементы будут сравниваться на втором этапе поиска второго по величине значения?


1.5.2.3

Найдите нижнюю границу числа сравнений при поиске по списку из N элементов. При обдумывании ответа постарайтесь представить себе, как выглядит дерево решений. (Подсказка: узлы должны быть помечены местоположением ключа.) Что можно сказать о числе необходимых для поиска сравнений, если упаковывать узлы настолько плотно, насколько это возможно?

Теги: